When a C# Windows Forms program starts, it displays a startup form. That form has a special place in the program's life cycle. If that form ever closes, the application ends.

The program can create and close as many other forms as it wants in any order without closing the program. The startup form is special in that respect.

When you click this example's New Form button, the following code displays a new instance of the main form.

// Display a new form with a blue background.
private void btnNewForm_Click(object sender, EventArgs e)
{
    Form1 frm = new Form1();
    frm.BackColor = Color.LightBlue;
    frm.Show();
}

This code simply creates a new instance of the form, sets its background color to light blue so you can distinguish the new forms from the startup form, and displays the form.

Run the program and create and close a few forms. Then create a form or two and close the startup form to see that the whole program stops.

This is not really much of a problem as long as you are aware of the situation.

So what can you do if you don't want the user to stop the application by closing the main form? This example uses the following FormClosing event handler to prevent the startup form from closing if any form's "Prevent Startup From Closing" CheckBox is checked.

// If this is the main form and any other forms have their
// Prevent Startup From Closing boxes checked, don't close.
private void Form1_FormClosing(object sender, FormClosingEventArgs e)
{
    // See if this is the main form.
    if (this == Application.OpenForms[0])
        // See if any form has the CheckBox checked.
        foreach (Form1 frm in Application.OpenForms)
            if (frm.chkPreventStartupFromClosing.Checked)
            {
                e.Cancel = true;
                break;
            }
}

If the form that is executing the FormClosing event handler is the startup form, then it is first in the Application object's OpenForms collection. If this is the startup form, then the code loops through all of the open forms. If the CheckBox on any open form is checked, then the event handler sets e.Cancel to true to prevent the form from closing.

   

In the picture, the program initially positioned the top form so it was hanging off the right and bottom edges of the screen. The program's code moved the form so it fit in the screen's lower right corner.

When you click this form's New Form button, the following code displays a new instance of the program's form.

// Position a new instance of this form
// just to the right and below the button.
private void btnShowForm_Click(object sender, EventArgs e)
{
    // Get the location in this form's coordinate system.
    Point form_pt = new Point(
        btnShowForm.Left + btnShowForm.Width / 2,
        btnShowForm.Top + btnShowForm.Height / 2);

    // Translate into the screen coordinate system.
    Point screen_pt = this.PointToScreen(form_pt);

    // Create the new form.
    Form1 frm = new Form1();

    // Make sure the form will be completely on the screen.
    Screen screen = Screen.FromControl(this);
    if (screen_pt.X < 0) screen_pt.X = 0;
    if (screen_pt.Y < 0) screen_pt.Y = 0;
    if (screen_pt.X > screen.WorkingArea.Right - frm.Width)
        screen_pt.X = screen.WorkingArea.Right - frm.Width;
    if (screen_pt.Y > screen.WorkingArea.Bottom - frm.Height)
        screen_pt.Y = screen.WorkingArea.Bottom - frm.Height;

    // Position the new form.
    frm.StartPosition = FormStartPosition.Manual;
    frm.Location = screen_pt;
    frm.Show();
}

The code makes a Point representing the center of the button. It calls PointToScreen to translate the point's coordinates to screen coordinates.

The code then creates a new form. It gets the Screen object that is displaying the form and adjusts the Point's coordinates to ensure that the form is completely on that Screen.

Finally the code sets the form's position and displays the form.

   

This is an issue if the user is using more than one monitor.

When this program starts, it uses the following code to get the Screen object that holds the form and display its device name, whether it is the primary screen, and its working area.

private void Form1_Load(object sender, EventArgs e)
{
    Screen screen = Screen.FromControl(this);
    txtDeviceName.Text = screen.DeviceName;
    txtIsPrimary.Text = screen.Primary.ToString();
    txtWorkingArea.Text = screen.WorkingArea.ToString();
    txtDeviceName.Select(0, 0);
}

The only non-obvious part of this code is the first statement where the program uses Screen.FromControl to get the Screen object holding the form.

   

When you click this example's button, the program uses the following code to display a new instance of the form positioned next to the button's lower left corner (as shown in the picture).

// Position a new instance of this form
// just to the right and below the button.
private void btnShowForm_Click(object sender, EventArgs e)
{
    // Get the location in this form's coordinate system.
    Point form_pt = new Point(btnShowForm.Right, btnShowForm.Bottom);

    // Translate into the screen coordinate system.
    Point screen_pt = this.PointToScreen(form_pt);

    // Create and position the form.
    Form1 frm = new Form1();
    frm.StartPosition = FormStartPosition.Manual;
    frm.Location = screen_pt;
    frm.Show();
}

The code creates a Point that holds the new form's desired location in this form's coordinate system. It then calls the form's PointToScreen method to convert the point into screen coordinates.

The code finishes by creating, positions, and displaying a new form. The only trick here is remembering to set the new form's StartPosition property to Manual so the form is positioned where its Location property says it should be.

   

This example extends the earlier one Apply filters to images to perform edge detection, smoothing, embossing, and more in C# by adding a new filter that embosses a color image without removing most of the color information. The filter's kernel is:

1	1	-1
1	1	-1
1	-1	-1

The kernel divides the result by 1 and uses no offset so it retains most of the image's color information. See the previous post for more information about how kernels work.

   

By default, the Debug and Trace class send messages to the Console window. Sometimes it might be nice to capture that text and save it in a file. This example shows how you can do that.

The Debug and Trace classes have a shared Listener collection that contains listener objects. The classes actually send their message to those objects not directly to the Console window. (Initially the Listeners collection contains a single listener that sends the text it receives to the Console window.)

You can remove the default listener from the collection if you like and you can add new listeners to the collection. This example uses the following code to add a TextWriterListener that appends the text it receives to a text file.

// Make the listener.
private void Form1_Load(object sender, EventArgs e)
{
    string trace_file = Application.StartupPath + "//trace.txt";
    Trace.Listeners.Add(new TextWriterTraceListener(trace_file));
    Trace.AutoFlush = true;
}

The code composes a file name. It then creates a TextWriterTraceListener, passing its constructor the file name, and adds the new listener to the Trace object's Listener collection. The Debug and Trace classes share Listeners collections so this listener will write both Trace and Debug messages into the file.

By default the Debug and Trace classes do not flush text buffers into text files so if the program ends without you explicitly flushing the output, some or all of the text may not be written into the file. The program avoids this problem by setting the Trace object's AutoFlush property to true.

If you enter a message in the program's TextBox and click Debug, the program executes the following code.

// Send a message to the Debug listeners.
private void btnDebug_Click(object sender, EventArgs e)
{
    Debug.WriteLine(txtMessage.Text);
    txtMessage.Clear();
    txtMessage.Focus();
}

This code uses the Debug.WriteLine method to send a message to the listeners. The default listener sends the text to the Console window and the other listener appends the text to the text file trace.txt.

   

(This method is similar to one that is described on my forthcoming book A Practical Introduction to Computer Algorithms. I'll post more about it later when it's closer to publication.)

The examples Recursively find the highest value path through a two-dimensional array of numbers in C# uses recursion to exhaustively search for the best possible path through the values in an array.

This is effective and reasonably simple but it can be very time consuming. There are roughly 3 choices at each row in the array (ignoring edge effects) and the program could start in any column. If the array has 14 rows and columns, then there are roughly 14 * 3¹⁴ = 66,961,566 possible paths. In fact there are 24,590,106 paths through that array, still a big number.

Branch and bound is a technique that lets you trim many of the paths from the search. As it recursively builds test solutions, the algorithm keeps track of the test solution's total value. At each step, it calculates the maximum amount by which the value could be increased. For this example, it multiples the number of rows it has not yet examined by the maximum possible value of an array entry and adds that to the test solution's value. it is unlikely that the test solution could actually be improved to that value but this gives an upper bound on the test solution's value. If the total maximum possible value is smaller than the value of the best solution found so far, then the algorithm stops considering that test solution.

This may seem like a small change that wouldn't remove many paths from the search, but it can be quite effective. You can see in the picture that in one trial branch and bound reduced the number of values recursively examined from more than 24 million to only 30 thousand.

The following code shows the new search method. The highlighted lines show differences between this version and the previous exhaustive search.

// Recursively explore paths starting with the indicated row.
// Return the path's total value.
private void FindPath2(int[] test_path, int test_total, int row)
{
    NumFindPathCalls++;

    // See if we have a complete solution.
    if (row >= NumRows)
    {
        // We have a complete solution.
        // See if it is better than the best solution so far.
        if (test_total > BestTotal2)
        {
            // This is an improvement.
            BestTotal2 = test_total;
            Array.Copy(test_path, BestPath2, NumRows);
        }
    }
    else
    {
        // We don't have a complete solution.

        // See if there's any chance we can improve
        // on the best solution found so far.
        int rows_remaining = NumRows - row;
        if (test_total + MaxValue * rows_remaining <= BestTotal2) return;

        // Try the possibilities for this row.

        // Get the column used in the previous row.
        int prev_col = test_path[row - 1];

        // Column - 1
        if (prev_col > 0)
        {
            int col = prev_col - 1;
            test_path[row] = col;
            FindPath2(test_path, test_total + Numbers[row, col], row + 1);
        }

        // Column
        test_path[row] = prev_col;
        FindPath2(test_path, test_total + Numbers[row, prev_col], row + 1);

        // Column + 1
        if (prev_col < NumCols - 1)
        {
            int col = prev_col + 1;
            test_path[row] = col;
            FindPath2(test_path, test_total + Numbers[row, col], row + 1);
        }
    }
}

The algorithm still searches a lot of paths so this only works up to a point. For larger problems, even it isn't fast enough and you'll need to use heuristics to search for approximate paths through the array.

(The example program's DisplayNumbers method also shows the branch and bound solution with red letters so you can compare it to the exhaustive solution that has a green background.)

   

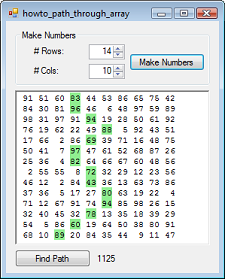(This method is similar to one that is described on my forthcoming book A Practical Introduction to Computer Algorithms. I'll post more about it later when it's closer to publication.)

Look at the picture on the right. The goal is to find a path through the array of numbers from the first row to the last row. When moving from one row to the next, you can move one column left or right, or keep the same column as the row above. The goal is to find the path that maximizes the total of the numbers visited.

The following code shows how the program makes the array of numbers when you click the Make Numbers button.

private void btnMakeNumbers_Click(object sender, EventArgs e)
{
    NumRows = (int)nudNumRows.Value;
    NumCols = (int)nudNumCols.Value;
    Numbers = new int[NumRows, NumCols];
    Random rand = new Random();
    for (int row = 0; row < NumRows; row++)
    {
        for (int col = 0; col < NumCols; col++)
        {
            Numbers[row, col] = rand.Next(1, 99);
        }
    }
    BestPath = null;

    // Display the numbers.
    DisplayNumbers();

    // Enable the Find Path button.
    btnFindPath.Enabled = true;
    lblTotal.Text = "";
}

The code reads the number of rows and columns you entered and then randomly generates the array of numbers. It then calls DisplayNumbers to display the numbers. I'll describe that method later after I explain how the program generates the best path.

The following FindBestPath method finds the best path through the array.

// The best path.
private int[] BestPath = null;
private int BestTotal = int.MinValue;

// Find the best path.
// Return the path's total value.
private int FindBestPath()
{
    // Make a test path, one entry per row.
    int[] test_path = new int[NumRows];

    // Start in row 0 and try each column.
    for (int col = 0; col < NumCols; col++)
    {
        test_path[0] = col;
        FindPath(test_path, 1);
    }

    // Return the best total.
    return BestTotal;
}

The method starts by creating a test_path array with one entry per row. It will hold the column used in each row.

The program then tries using each column as the first number visited. For each column, it fills in that column number in test_path[0] and then calls the following FindPath method to explore solutions that begin with that first column.

// Recursively explore paths starting with the indicated row.
// Return the path's total value.
private void FindPath(int[] test_path, int row)
{
    // See if we have a complete solution.
    if (row >= NumRows)
    {
        // We have a complete solution.
        // See if it is better than the best solution so far.
        int total = 0;
        for (int r = 0; r < NumRows; r++) total += Numbers[r, test_path[r]];
        if (total > BestTotal)
        {
            // This is an improvement.
            BestTotal = total;
            Array.Copy(test_path, BestPath, NumRows);
        }
    }
    else
    {
        // We don't have a complete solution.
        // Try the possibilities for this row.

        // Get the column used in the previous row.
        int prev_col = test_path[row - 1];

        // Column - 1
        if (prev_col > 0)
        {
            test_path[row] = prev_col - 1;
            FindPath(test_path, row + 1);
        }

        // Column
        test_path[row] = prev_col;
        FindPath(test_path, row + 1);

        // Column + 1
        if (prev_col < NumCols - 1)
        {
            test_path[row] = prev_col + 1;
            FindPath(test_path, row + 1);
        }
    }
}

The FindPath method does the most interesting work. It recursively fills in the test_path array. When the array is completely full, it checks the test solution's value to see if it is an improvement over the current best solution.

The method starts by checking its row parameter to see if the test solution is complete. If row >= NumRows, then the method has been called to fill in the entry for the row after the last row in the array. That means the test array is full so the method adds up the total value of the solution, compares it to the best solution found so far, and saves it if this is an improvement.

If the test solution is not complete, the method tries each of the three possible values for the column in this row and then recursively calls itself to try values for the rest of the test solution's rows. (Eventually the recursive calls fill in all of the rows' values and previous case occurs so the method checks for an improved solution.)

That's all there is to finding the best solution. The following code shows how the program displays the numbers and the best solution, if there is one.

// Display the numbers and the best path.
private void DisplayNumbers()
{
    // Display the numbers.
    string txt = "";
    for (int row = 0; row < NumRows; row++)
    {
        txt += Environment.NewLine;
        for (int col = 0; col < NumCols; col++)
        {
            txt += string.Format("{0,3}", Numbers[row, col]);
        }
    }
    txt = txt.Substring(Environment.NewLine.Length);
    rchNumbers.Text = txt;

    // Display the best path.
    if (BestPath == null) return;
    rchNumbers.Select();
    rchNumbers.SelectionBackColor = Color.White;
    for (int row = 0; row < NumRows; row++)
    {
        int start = 1 +
            row * (NumCols * 3 + Environment.NewLine.Length - 1) +
            BestPath[row] * 3;
        rchNumbers.Select(start, 2);
        rchNumbers.SelectionBackColor = Color.LightGreen;
    }
    rchNumbers.Select(0, 0);

    // Display the best path in the Console window.
    for (int row = 0; row < NumRows; row++)
        Console.Write(Numbers[row, BestPath[row]] + " ");
    Console.WriteLine("");            
}

The code first loops through the numbers a builds a multiline string that contains them all. It sets the rchNumbers RichTextBox's Text property to the result.

Next the code gives the RichTextBox a white background. It then loops over the rows. For each row, it gets the column that is part of the best solution and calculates the location of that row and column in the text. It selects the corresponding text and sets the RichTextBox's background color to light green for the selection.

The moves the RichTextBox's selection point to the beginning of the text so nothing is shown as selected. It finishes by displaying the values selected in the best solution in the Console window so you can verify that the highlighted values match the best solution.

This technique of building a solution by recursively trying every possibility for each of the required entries is quite powerful. You can use this method to solve many hard problems, although it requires you to look at a lot of potential solutions so it only works for relatively small problems. (My book talks more about this and explains some approaches you can use to solve larger problems.)

   

This example extends the example Write data into an Excel workbook in C#. See that example for information on how to open an Excel workbook, write data into it, and save it.

Note that before you can use the Excel interop library, you need to open the Add References dialog, click the COM tab, and select Microsoft Excel 12.0 Object Library (or whatever version you have installed on your system.)

After opening the workbook and writing data into it as shown in the earlier example, this example uses the following code to save the active worksheet in a PDF file.

// Save into a PDF.
string filename = txtFile.Text.Replace(".xlsx", ".pdf");
const int xlQualityStandard = 0;
sheet.ExportAsFixedFormat(
    Excel.XlFixedFormatType.xlTypePDF,
    filename, xlQualityStandard, true, false,
    Type.Missing, Type.Missing, true, Type.Missing);

This code converts the Excel workbook's file name into a file name with the .pdf extension. It then calls the active worksheet's ExportAsFixedFormat method to export the data into PDF format. If you open the project in Visual Studio, IntelliSense will give you the names of the parameters to ExportAsFixedFormat.

The program then finishes by closing Excel.

Much of the work in this kind of Office automation is figuring out what objects in the Office object model do the things you want. For example, figuring out how to use Word's InlineShape and Shape objects to create and format the picture. If you want to do a lot of this, my book Microsoft Office Programming: A Guide for Experienced Developers may help. The code is in Visual Basic and it's a few years old but it should help you figure out how to manipulate the Word, Excel, PowerPoint, Access, and Outlook object models and those models haven't changed too much since the book was written.

   

Sometimes it's useful to use a non-standard cursor in a program. This example explains how you can load a cursor from a cursor file included as a project resource.

To add a cursor file to the project's resources, open the Project menu and select Properties. On the Resources tab, open the Add Resource dropdown and select Add Existing File. Select the file and click Open.

Noe use code similar to the following to load the cursor resource at run time.

// Load the cursors from resources.
private void Form1_Load(object sender, EventArgs e)
{
    pictureBox1.Cursor = new Cursor(new MemoryStream(Properties.Resources.AddLink1));
    pictureBox2.Cursor = new Cursor(new MemoryStream(Properties.Resources._4WAY03));
    pictureBox3.Cursor = new Cursor(new MemoryStream(Properties.Resources.BULLSEYE));
}

The MemoryStream class is in the System.IO namespace. You can make it easier to use by adding this statement at the top of the file.

using System.IO;